Note

This notebook is executed during documentation build to show live results. You can also run it interactively on Binder.

Plateau Diagnostics Demo

This notebook demonstrates the use of isotonic regression plateau diagnostics to distinguish between noise-based flattening (good) and limited-data flattening (bad).

Overview

When isotonic regression creates flat regions (plateaus) in calibration curves, it could be for two reasons:

1. Noise-based flattening (good): Adjacent scores truly have similar risks, and pooling reduces variance without losing meaningful resolution.

2. Limited-data flattening (bad): Adjacent scores have different risks, but the calibration sample is too small to detect the difference.

This package provides comprehensive diagnostics to help distinguish between these cases.

import matplotlib.pyplot as plt
import numpy as np
from sklearn.isotonic import IsotonicRegression
from sklearn.model_selection import train_test_split

# Import calibre diagnostics (updated for v0.4.1)
from calibre import (
    IsotonicCalibrator,
    NearlyIsotonicCalibrator,
    RegularizedIsotonicCalibrator,
    run_plateau_diagnostics,
)

# Import metrics (updated for v0.4.1)
from calibre.metrics import (
    calibration_diversity_index,
    plateau_quality_score,
    progressive_sampling_diversity,
    tie_preservation_score,
)

# Import visualization (optional)
try:
    from calibre.visualization import (
        plot_calibration_comparison,
        plot_plateau_diagnostics,
        plot_progressive_sampling,
    )

    HAS_VIZ = True
except ImportError:
    print(
        "Visualization module requires matplotlib. Install with: pip install matplotlib"
    )
    HAS_VIZ = False

np.random.seed(42)
print("Calibre plateau diagnostics demo loaded successfully!")

Calibre plateau diagnostics demo loaded successfully!

1. Generate Synthetic Data

Let’s create two scenarios:

• Scenario A: Data with genuine flat regions (noise-based flattening)

• Scenario B: Data with smooth trends but small sample size (limited-data flattening)

def create_genuine_plateau_data(n=200, noise_level=0.05):
    """Create data with genuine flat regions."""
    X = np.sort(np.random.uniform(0, 1, n))

    # Create true probabilities with intentional flat regions
    y_true = np.zeros(n)
    y_true[: n // 4] = 0.1  # Flat low region
    y_true[n // 4 : n // 2] = np.linspace(0.1, 0.4, n // 4)  # Rising
    y_true[n // 2 : 3 * n // 4] = 0.4  # Flat middle region
    y_true[3 * n // 4 :] = np.linspace(0.4, 0.8, n // 4)  # Rising

    # Add small amount of noise
    y_true += np.random.normal(0, noise_level, n)
    y_true = np.clip(y_true, 0, 1)

    # Generate binary outcomes
    y_binary = np.random.binomial(1, y_true)

    return X, y_binary, y_true


def create_smooth_small_data(n=50):
    """Create smooth data with small sample size."""
    X = np.sort(np.random.uniform(0, 1, n))

    # Smooth sigmoid-like curve
    y_true = 1 / (1 + np.exp(-8 * (X - 0.5)))

    # Generate binary outcomes
    y_binary = np.random.binomial(1, y_true)

    return X, y_binary, y_true


# Generate both scenarios
X_genuine, y_genuine, y_true_genuine = create_genuine_plateau_data()
X_small, y_small, y_true_small = create_smooth_small_data()

print(f"Genuine plateau data: {len(X_genuine)} samples")
print(f"Small sample data: {len(X_small)} samples")

Genuine plateau data: 200 samples
Small sample data: 50 samples

2. Basic Isotonic Regression with Diagnostics

Let’s start with the simple wrapper that automatically runs diagnostics:

# Scenario A: Genuine plateaus (updated for v0.4.1)
print("=== Scenario A: Genuine Plateau Data ===")
cal_genuine = IsotonicCalibrator(enable_diagnostics=True)
cal_genuine.fit(X_genuine, y_genuine)

print("\nDiagnostic Summary:")
if cal_genuine.has_diagnostics():
    print(cal_genuine.diagnostic_summary())
else:
    print("No diagnostics available")

# Get calibrated predictions
y_cal_genuine = cal_genuine.transform(X_genuine)

=== Scenario A: Genuine Plateau Data ===

Diagnostic Summary:
Detected 7 plateau(s):

Warnings:
  ⚠ Plateau 4 at [0.817, 0.832] has only 4 samples - may be unreliable
  ⚠ Plateau 7 at [0.972, 0.987] has only 3 samples - may be unreliable

# Scenario B: Small sample data (updated for v0.4.1)
print("=== Scenario B: Small Sample Data ===")
cal_small = IsotonicCalibrator(enable_diagnostics=True)
cal_small.fit(X_small, y_small)

print("\nDiagnostic Summary:")
if cal_small.has_diagnostics():
    print(cal_small.diagnostic_summary())
else:
    print("No diagnostics available")

y_cal_small = cal_small.transform(X_small)

=== Scenario B: Small Sample Data ===

Diagnostic Summary:
Detected 5 plateau(s):

Warnings:
  ⚠ Plateau 1 at [0.052, 0.102] has only 3 samples - may be unreliable
  ⚠ Plateau 4 at [0.533, 0.581] has 5 samples - consider collecting more data in this range

3. Advanced Diagnostic Analysis

For more detailed analysis, we can use the IsotonicDiagnostics class directly:

# Split data for more thorough analysis (train/test)
X_train, X_test, y_train, y_test = train_test_split(
    X_genuine, y_genuine, test_size=0.3, random_state=42
)

# Run comprehensive diagnostics using standalone function (updated for v0.4.1)
# First fit calibrator and get predictions
cal = IsotonicCalibrator()
cal.fit(X_train, y_train)
y_cal_train = cal.transform(X_train)

# Run plateau diagnostics on the calibrated results
results = run_plateau_diagnostics(X_train, y_train, y_cal_train)

print("Detailed diagnostic results:")
print(f"Detected {results['n_plateaus']} plateau regions")

if results['n_plateaus'] > 0:
    print("\nPlateau details:")
    for i, plateau in enumerate(results['plateaus']):
        print(f"  Plateau {i + 1}:")
        if 'x_range' in plateau:
            print(f"    X range: [{plateau['x_range'][0]:.3f}, {plateau['x_range'][1]:.3f}]")
        if 'value' in plateau:
            print(f"    Value: {plateau['value']:.3f}")
        if 'n_samples' in plateau:
            print(f"    Samples: {plateau['n_samples']}")
        if 'sample_density' in plateau:
            print(f"    Density: {plateau['sample_density']}")

if results['warnings']:
    print("\nWarnings:")
    for warning in results['warnings']:
        print(f"  ⚠️  {warning}")

Detailed diagnostic results:
Detected 6 plateau regions

Plateau details:
  Plateau 1:
    X range: [0.007, 0.051]
    Value: 0.111
    Samples: 9
    Density: sparse
  Plateau 2:
    X range: [0.058, 0.242]
    Value: 0.273
    Samples: 33
    Density: adequate
  Plateau 3:
    X range: [0.242, 0.832]
    Value: 0.365
    Samples: 74
    Density: adequate
  Plateau 4:
    X range: [0.835, 0.897]
    Value: 0.571
    Samples: 7
    Density: sparse
  Plateau 5:
    X range: [0.897, 0.970]
    Value: 0.857
    Samples: 14
    Density: adequate
  Plateau 6:
    X range: [0.986, 0.987]
    Value: 1.000
    Samples: 2
    Density: very_sparse

Warnings:
  ⚠️  Plateau 1 at [0.007, 0.051] has 9 samples - consider collecting more data in this range
  ⚠️  Plateau 4 at [0.835, 0.897] has 7 samples - consider collecting more data in this range
  ⚠️  Plateau 6 at [0.986, 0.987] has only 2 samples - may be unreliable

4. Diagnostic Metrics

Let’s explore the specific diagnostic metrics:

# Compare original vs calibrated predictions
iso_basic = IsotonicRegression()
iso_basic.fit(X_genuine, y_genuine)
y_cal_basic = iso_basic.transform(X_genuine)

# Tie preservation score
tie_score = tie_preservation_score(X_genuine, y_cal_basic)
print(f"Tie preservation score: {tie_score:.3f}")

# Plateau quality score
quality_score = plateau_quality_score(X_genuine, y_genuine, y_cal_basic)
print(f"Plateau quality score: {quality_score:.3f}")

# Calibration diversity
diversity_orig = calibration_diversity_index(X_genuine)
diversity_cal = calibration_diversity_index(y_cal_basic)
diversity_relative = calibration_diversity_index(y_cal_basic, diversity_orig)

print(f"Original diversity: {diversity_orig:.3f}")
print(f"Calibrated diversity: {diversity_cal:.3f}")
print(f"Relative diversity: {diversity_relative:.3f}")

Tie preservation score: 0.642
Plateau quality score: 0.423
Original diversity: 1.000
Calibrated diversity: 0.040
Relative diversity: 0.040

5. Progressive Sampling Analysis

This helps distinguish limited-data flattening by showing how diversity changes with sample size:

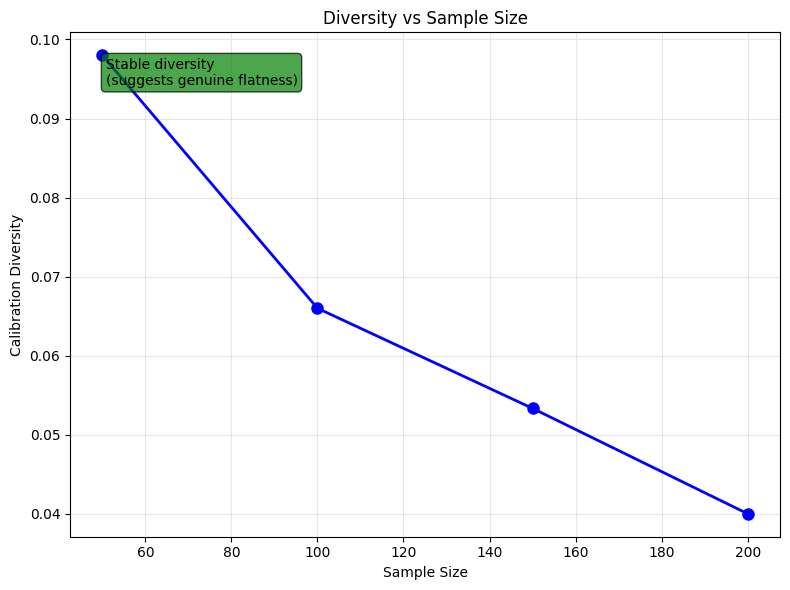
# Progressive sampling analysis
sample_sizes, diversities = progressive_sampling_diversity(
    X_genuine, y_genuine, sample_sizes=[50, 100, 150, 200], n_trials=10, random_state=42
)

print("Progressive sampling results:")
for size, div in zip(sample_sizes, diversities):
    print(f"  Sample size {size}: diversity = {div:.3f}")

# Interpret trend
slope = (diversities[-1] - diversities[0]) / (sample_sizes[-1] - sample_sizes[0])
if slope > 0.001:
    print(
        "\nInterpretation: Increasing diversity suggests potential limited-data flattening"
    )
elif slope < -0.001:
    print("\nInterpretation: Decreasing diversity (unusual pattern)")
else:
    print("\nInterpretation: Stable diversity suggests genuine flatness")

Progressive sampling results:
  Sample size 50: diversity = 0.098
  Sample size 100: diversity = 0.066
  Sample size 150: diversity = 0.053
  Sample size 200: diversity = 0.040

Interpretation: Stable diversity suggests genuine flatness

6. Comparison with Alternative Methods

Let’s compare strict isotonic regression with softer alternatives:

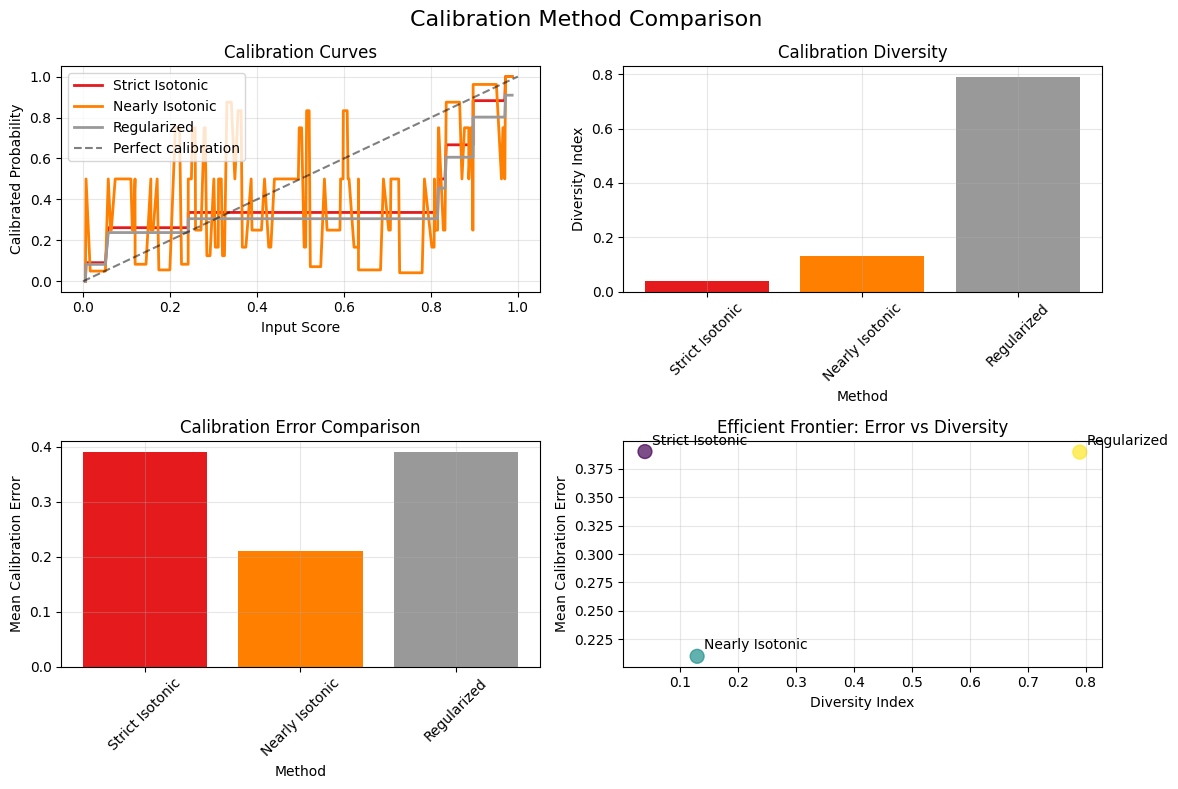
# Compare different calibration methods (updated for v0.4.1)
from calibre.metrics import mean_calibration_error

# Fit different calibrators
iso_strict = IsotonicCalibrator()
iso_nearly = NearlyIsotonicCalibrator(lam=1.0)
iso_reg = RegularizedIsotonicCalibrator(alpha=0.1)

calibrators = {
    "Strict Isotonic": iso_strict.fit(X_genuine, y_genuine),
    "Nearly Isotonic": iso_nearly.fit(X_genuine, y_genuine),
    "Regularized": iso_reg.fit(X_genuine, y_genuine),
}

# Compare diversity and calibration error
print("Method comparison:")
for name, cal in calibrators.items():
    try:
        y_pred = cal.transform(X_genuine)
        diversity = calibration_diversity_index(y_pred)
        error = mean_calibration_error(y_genuine, y_pred)
        n_unique = len(np.unique(y_pred))

        print(f"  {name}:")
        print(f"    Diversity: {diversity:.3f}")
        print(f"    Calibration error: {error:.3f}")
        print(f"    Unique values: {n_unique}/{len(y_pred)}")
    except Exception as e:
        print(f"  {name}: Error - {e}")

Method comparison:
  Strict Isotonic:
    Diversity: 0.040
    Calibration error: 0.390
    Unique values: 8/200
  Nearly Isotonic:
    Diversity: 0.130
    Calibration error: 0.210
    Unique values: 26/200
  Regularized:
    Diversity: 0.790
    Calibration error: 0.390
    Unique values: 158/200

7. Visualization (if matplotlib available)

Let’s create some visualizations to better understand the diagnostics:

# Visualization
try:
    if HAS_VIZ:
        # Try to plot comprehensive diagnostic results
        # Note: visualization module may have compatibility issues with current data format
        y_cal_for_plot = iso_strict.transform(X_genuine)

        # Skip plot_plateau_diagnostics as it expects different data format
        print("Visualization of plateau diagnostics (text version):")
        if results['n_plateaus'] > 0:
            for i, plateau in enumerate(results['plateaus']):
                print(f"  Plateau {i+1}: X=[{plateau['x_range'][0]:.3f}, {plateau['x_range'][1]:.3f}], "
                      f"Y={plateau['value']:.3f}, Samples={plateau['n_samples']}, "
                      f"Density={plateau['sample_density']}")

        # Try progressive sampling plot if available
        try:
            fig2 = plot_progressive_sampling(sample_sizes, diversities)
            plt.show()
        except Exception as e:
            print(f"Progressive sampling plot not available: {e}")

        # Try calibration comparison plot if available
        try:
            fig3 = plot_calibration_comparison(X_genuine, y_genuine, calibrators)
            plt.show()
        except Exception as e:
            print(f"Calibration comparison plot not available: {e}")
    else:
        print("Visualization not available. Install matplotlib to see plots.")
except Exception as e:
    print(f"Visualization error: {e}")

# Always provide text-based visualization as fallback
print("\nSimple calibration curve comparison:")
X_sample = X_genuine[::10]  # Sample every 10th point

for name, cal in calibrators.items():
    try:
        y_sample = cal.transform(X_sample)
        print(f"\n{name}:")
        for i in range(0, min(5, len(X_sample)), 1):
            print(f"  X={X_sample[i]:.2f} -> Y={y_sample[i]:.3f}")
    except Exception as e:
        print(f"{name}: Error - {e}")

Visualization of plateau diagnostics (text version):
  Plateau 1: X=[0.007, 0.051], Y=0.111, Samples=9, Density=sparse
  Plateau 2: X=[0.058, 0.242], Y=0.273, Samples=33, Density=adequate
  Plateau 3: X=[0.242, 0.832], Y=0.365, Samples=74, Density=adequate
  Plateau 4: X=[0.835, 0.897], Y=0.571, Samples=7, Density=sparse
  Plateau 5: X=[0.897, 0.970], Y=0.857, Samples=14, Density=adequate
  Plateau 6: X=[0.986, 0.987], Y=1.000, Samples=2, Density=very_sparse

Simple calibration curve comparison:

Strict Isotonic:
  X=0.01 -> Y=0.000
  X=0.05 -> Y=0.091
  X=0.09 -> Y=0.262
  X=0.14 -> Y=0.262
  X=0.18 -> Y=0.262

Nearly Isotonic:
  X=0.01 -> Y=0.000
  X=0.05 -> Y=0.050
  X=0.09 -> Y=0.500
  X=0.14 -> Y=0.083
  X=0.18 -> Y=0.056

Regularized:
  X=0.01 -> Y=0.000
  X=0.05 -> Y=0.083
  X=0.09 -> Y=0.238
  X=0.14 -> Y=0.238
  X=0.18 -> Y=0.238

8. Practical Decision Framework

Based on the diagnostic results, here’s how to make practical decisions:

def recommend_calibration_method(diagnostic_results, diversity_trend_slope=None):
    """Provide calibration method recommendations based on diagnostics."""

    if diagnostic_results['n_plateaus'] == 0:
        return "Standard isotonic regression (no plateaus detected)"

    # Count plateau types based on sample density
    concerning = 0
    total = diagnostic_results['n_plateaus']

    for plateau in diagnostic_results['plateaus']:
        if 'sample_density' in plateau:
            if plateau['sample_density'] in ['sparse', 'very_sparse']:
                concerning += 1

    recommendations = []

    if concerning == 0:
        recommendations.append(
            "✅ Standard isotonic regression (all plateaus appear genuine)"
        )
    elif concerning / total > 0.5:
        recommendations.append("⚠️  Consider softer calibration methods:")
        recommendations.append(
            "   - Nearly isotonic regression (allows small violations)"
        )
        recommendations.append("   - Regularized isotonic regression")
        recommendations.append("   - Spline calibration")
    else:
        recommendations.append("🤔 Mixed evidence - consider:")
        recommendations.append("   - Cross-validation between strict and soft methods")
        recommendations.append("   - Collecting more calibration data if possible")

    # Additional recommendations based on diversity trend
    if diversity_trend_slope is not None:
        if diversity_trend_slope > 0.001:
            recommendations.append(
                "📈 Increasing diversity with sample size suggests limited-data flattening"
            )
            recommendations.append(
                "   -> Strongly recommend collecting more data or using softer methods"
            )
        elif diversity_trend_slope < -0.001:
            recommendations.append(
                "📉 Unusual decreasing diversity pattern - investigate data quality"
            )

    return "\n".join(recommendations)


# Get recommendations for our data (updated for v0.4.1)
slope = (diversities[-1] - diversities[0]) / (sample_sizes[-1] - sample_sizes[0])
recommendations = recommend_calibration_method(results, slope)

print("=== CALIBRATION METHOD RECOMMENDATIONS ===")
print(recommendations)

=== CALIBRATION METHOD RECOMMENDATIONS ===
🤔 Mixed evidence - consider:
   - Cross-validation between strict and soft methods
   - Collecting more calibration data if possible

9. Summary and Best Practices

Key Diagnostic Indicators:

1. Tie Stability (Bootstrap):

   • High (>0.7): Suggests genuine flatness

   • Low (<0.3): Suggests limited-data flattening

2. Conditional AUC Among Tied Pairs:

   • Close to 0.5: Supports noise-based flattening

   • Much above 0.5: Suggests limited-data flattening

3. Progressive Sampling Diversity:

   • Stable: Supports genuine flatness

   • Increasing: Suggests limited-data flattening

4. Minimum Detectable Difference (MDD):

   • Compare with domain knowledge of plausible effect sizes

Best Practices:

1. Always run diagnostics when using isotonic regression

2. Use multiple diagnostic criteria together, not individually

3. Consider domain knowledge about expected effect sizes

4. Cross-validate between strict and soft calibration methods

5. Collect more data when limited-data flattening is suspected

6. Document your calibration decisions based on diagnostic evidence

print("🎉 Plateau diagnostics demo completed!")
print("\nKey takeaways:")
print("1. Not all plateaus are created equal")
print("2. Diagnostics help distinguish genuine vs. artifactual flattening")
print("3. Multiple complementary tests provide robust evidence")
print("4. Consider both statistical and domain-specific evidence")
print("5. When in doubt, prefer softer calibration methods")

🎉 Plateau diagnostics demo completed!

Key takeaways:
1. Not all plateaus are created equal
2. Diagnostics help distinguish genuine vs. artifactual flattening
3. Multiple complementary tests provide robust evidence
4. Consider both statistical and domain-specific evidence
5. When in doubt, prefer softer calibration methods