User Guide¶

This comprehensive guide covers all aspects of using optimal-classification-cutoffs effectively.

Understanding Classification Thresholds¶

Most machine learning classifiers output probabilities or scores that need to be converted to discrete predictions. The default threshold of 0.5 is often suboptimal, especially for:

Imbalanced datasets: When one class is much more frequent than others
Cost-sensitive applications: When different types of errors have different consequences
Specific metric optimization: When you need to maximize F1, precision, recall, or other metrics

Why Standard Methods Fail¶

Classification metrics like F1 score, accuracy, precision, and recall are piecewise-constant functions with respect to the decision threshold. This creates challenges for traditional optimization:

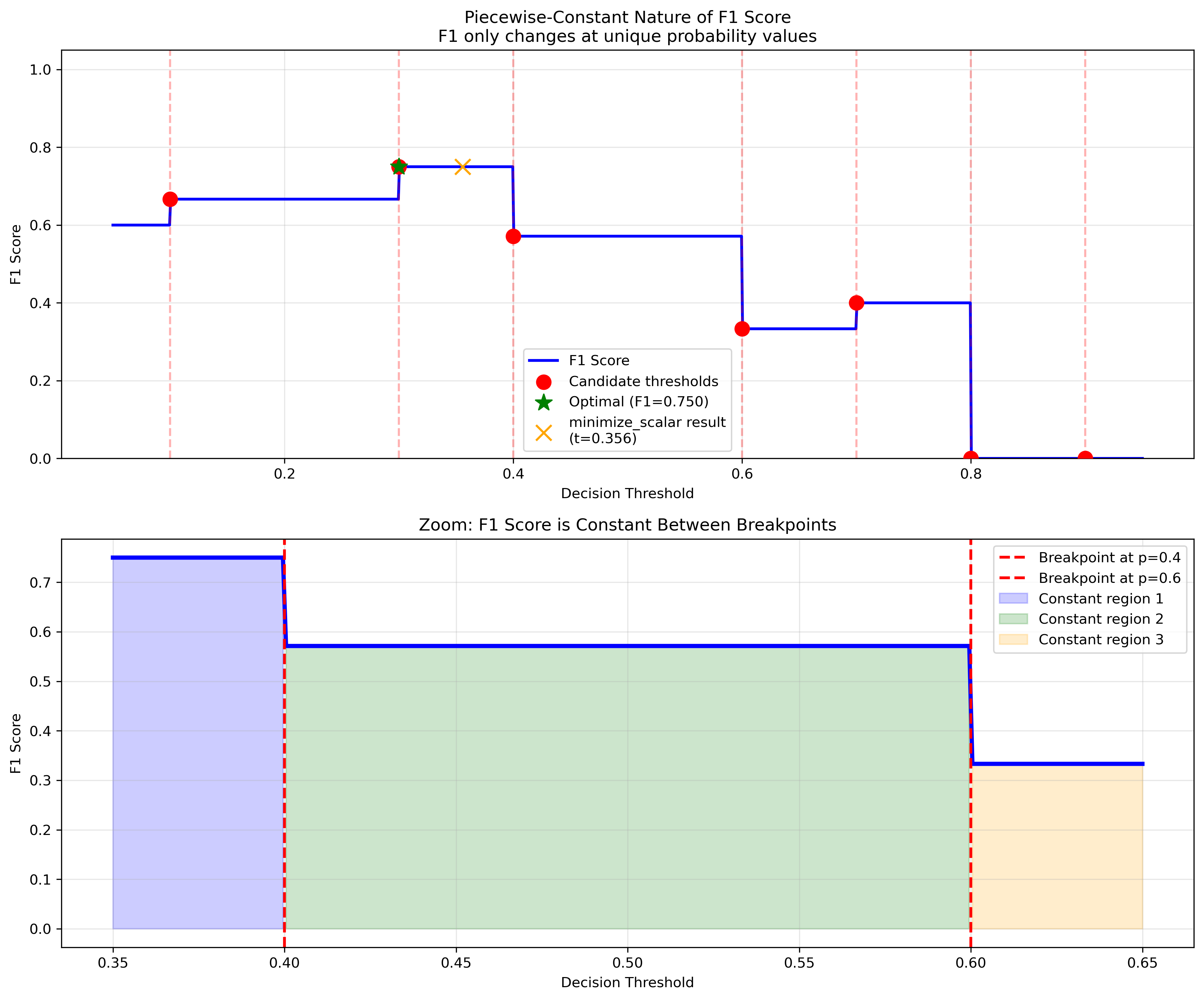
Standard optimization methods assume smooth, differentiable functions, but classification metrics:

Have zero gradients almost everywhere
Only change values at specific threshold points
Can trap gradient-based optimizers in suboptimal regions

Binary Classification¶

Basic Usage¶

from optimal_cutoffs import optimize_thresholds
import numpy as np

# Your classification results
y_true = np.array([0, 0, 1, 1, 0, 1, 1, 0])
y_prob = np.array([0.1, 0.4, 0.35, 0.8, 0.2, 0.9, 0.7, 0.3])

# Find optimal threshold
result = optimize_thresholds(y_true, y_prob, metric='f1')
print(f"Optimal threshold: {result.threshold:.3f}")
print(f"Expected F1: {result.scores[0]:.3f}")

# Make predictions
predictions = result.predict(y_prob)

Supported Metrics¶

Built-in metrics include:

'f1': F1 score (harmonic mean of precision and recall)
'accuracy': Classification accuracy
'precision': Positive predictive value
'recall': Sensitivity, true positive rate

# Compare thresholds for different metrics
metrics = ['f1', 'accuracy', 'precision', 'recall']
for metric in metrics:
    result = optimize_thresholds(y_true, y_prob, metric=metric)
    print(f"{metric}: {result.thresholds[0]:.3f}")

Optimization Methods¶

The library provides several optimization strategies:

Auto Selection (Recommended)

result = optimize_thresholds(y_true, y_prob, metric='f1', method='auto')

The auto method intelligently selects the best algorithm based on the metric properties and data size.

Sort-Scan Algorithm

result = optimize_thresholds(y_true, y_prob, metric='f1', method='sort_scan')

O(n log n) exact optimization for piecewise metrics. Fastest for large datasets.

Minimize Algorithm

result = optimize_thresholds(y_true, y_prob, metric='f1', method='minimize')

Uses scipy optimization with enhanced fallbacks for robustness.

Comparison Operators¶

Control how threshold comparisons are handled:

# Exclusive comparison: prediction = 1 if prob > threshold
result = optimize_thresholds(y_true, y_prob, metric='f1', comparison='>')

# Inclusive comparison: prediction = 1 if prob >= threshold
result = optimize_thresholds(y_true, y_prob, metric='f1', comparison='>=')

This is important when many probability values are tied or at exact threshold boundaries.

Sample Weights¶

Handle imbalanced datasets or assign different importance to samples:

# Create sample weights (e.g., inverse frequency weighting)
sample_weights = np.array([2.0, 2.0, 0.5, 0.5, 2.0, 0.5, 0.5, 2.0])

result = optimize_thresholds(
    y_true, y_prob, metric='f1',
    sample_weight=sample_weights
)

Multiclass Classification¶

The library automatically detects multiclass problems and uses One-vs-Rest strategy:

# 3-class example
y_true = np.array([0, 1, 2, 0, 1, 2, 0, 1])
y_prob = np.array([
    [0.8, 0.1, 0.1],  # Strongly class 0
    [0.2, 0.7, 0.1],  # Strongly class 1
    [0.1, 0.2, 0.7],  # Strongly class 2
    [0.6, 0.3, 0.1],  # Moderately class 0
    [0.1, 0.8, 0.1],  # Strongly class 1
    [0.1, 0.1, 0.8],  # Strongly class 2
    [0.5, 0.4, 0.1],  # Weakly class 0
    [0.3, 0.6, 0.1],  # Moderately class 1
])

# Returns array of per-class thresholds
result = optimize_thresholds(y_true, y_prob, metric='f1')
print(f"Class thresholds: {result.thresholds}")

Multiclass Averaging¶

Control how metrics are aggregated across classes:

# Macro averaging: equal weight to all classes
result = optimize_thresholds(y_true, y_prob, metric='f1', average='macro')

# Weighted averaging: weight by class frequency
result = optimize_thresholds(y_true, y_prob, metric='f1', average='weighted')

Making Predictions¶

Convert multiclass probabilities to predictions using optimized thresholds:

from optimal_cutoffs import ThresholdOptimizer

# Fit optimizer
optimizer = ThresholdOptimizer(metric='f1')
optimizer.fit(y_true, y_prob)

# Make predictions on new data
y_pred = optimizer.predict(y_prob_new)

Cost-Sensitive Optimization¶

For applications where different errors have different costs or benefits:

Basic Cost Specification¶

# False negatives cost 5x more than false positives
result = optimize_thresholds(
    y_true, y_prob,
    utility={"fp": -1.0, "fn": -5.0}
)

Complete Utility Matrix¶

# Specify utilities for all outcomes
result = optimize_thresholds(
    y_true, y_prob,
    utility={
        "tp": 10.0,   # Benefit for correct positive prediction
        "tn": 1.0,    # Benefit for correct negative prediction
        "fp": -2.0,   # Cost for false positive
        "fn": -50.0   # Cost for false negative
    }
)

Bayes-Optimal Thresholds¶

For calibrated probabilities, calculate theoretical optimum without training data:

# Bayes-optimal threshold (no training labels needed)
result = optimize_thresholds(
    None, y_prob,  # None for true labels
    utility={"fp": -1.0, "fn": -5.0},
    mode="bayes"
)

Cross-Validation¶

Robust threshold estimation using cross-validation:

from optimal_cutoffs.cv import cross_validate

# 5-fold cross-validation
cv_results = cross_validate(
    y_true, y_prob,
    metric='f1',
    cv=5,
    method='auto'
)
thresholds = cv_results['thresholds']
scores = cv_results['scores']

print(f"CV thresholds: {thresholds}")
print(f"CV scores: {scores}")
print(f"Mean threshold: {np.mean(thresholds):.3f}")

Custom Metrics¶

from optimal_cutoffs.metrics import register_metric

def custom_metric(tp, tn, fp, fn):
    """Custom metric: weighted combination of precision and recall."""
    precision = tp / (tp + fp) if tp + fp > 0 else 0.0
    recall = tp / (tp + fn) if tp + fn > 0 else 0.0
    return 0.7 * precision + 0.3 * recall

# Register the metric
register_metric('custom', custom_metric)

# Use it for optimization
result = optimize_thresholds(y_true, y_prob, metric='custom')

Performance Considerations¶

Method Selection Guidelines¶

Small datasets (< 1,000 samples): Use method='minimize'
Large datasets: Use method='auto' or method='sort_scan'
High precision needs: Use method='sort_scan' for exact results
Speed critical: Use method='sort_scan' for piecewise metrics

Memory Usage¶

For very large datasets:

# Process in chunks for memory efficiency
chunk_size = 10000
thresholds = []

for i in range(0, len(y_true), chunk_size):
    chunk_true = y_true[i:i+chunk_size]
    chunk_prob = y_prob[i:i+chunk_size]

    result = optimize_thresholds(
        chunk_true, chunk_prob,
        metric='f1', method='sort_scan'
    )
    threshold = result.thresholds[0]
    thresholds.append(threshold)

# Combine results (example: take median)
final_threshold = np.median(thresholds)

Best Practices¶

Data Quality¶

Ensure probability calibration: Use Platt scaling or isotonic regression if needed
Handle class imbalance: Use sample weights or stratified sampling
Validate on held-out data: Always test thresholds on independent data

Threshold Selection¶

Consider multiple metrics: Optimize for the metric that matters for your application
Use cross-validation: Get robust threshold estimates with uncertainty quantification
Account for costs: Use utility-based optimization when error costs are known

Integration¶

Use ThresholdOptimizer: For scikit-learn compatibility and clean APIs
Save thresholds: Store optimized thresholds with your trained models
Monitor performance: Track threshold effectiveness in production